II. Dessiner▲
II-A. L'espace de dessin▲
L'espace de dessin constitue l'espace de représentation proprement dit. Cette fenêtre de visualisation affichera vos réalisations dans Processing en deux ou trois dimensions.
Cet espace est créé par l'instruction size() qui prend deux arguments : size(largeur,hauteur);.
Par exemple, dans la fenêtre d'édition du logiciel Processing, saisissez la commande suivante :

Puis cliquez sur le bouton run, votre fenêtre de visualisation se créé :

Amusez-vous à changer les dimensions de cette fenêtre en modifiant les valeurs entre parenthèses pour en voir le résultat.
Par défaut :
size();
…affichera une fenêtre de 100 pixels sur 100 pixels.
Félicitations, vous avez créé votre première fenêtre de visualisation !
II-A-1. Coordonnées dans l'espace▲
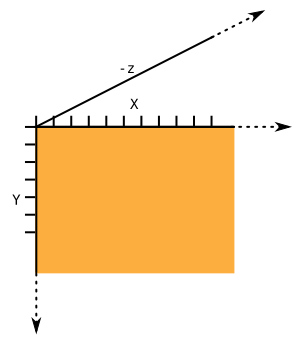
Quand on travaille en deux dimensions (2D), on utilise deux axes de coordonnées x et y correspondant respectivement à la largeur (axe horizontal) et à la hauteur (axe vertical) d'une situation. Par convention de la mesure de l'espace, le coin en haut à gauche correspond aux valeurs x=0 et y=0. Les valeurs x sont croissantes vers la droite et les valeurs y sont croissantes vers le bas, contrairement à notre habitude du plan cartésien. Ces valeurs x et y peuvent s'étendre théoriquement à l'infini, même si, en réalité, les contraintes de la taille de votre fenêtre vont délimiter la taille maximale d'une surface de création visible. C'est donc dans cet espace que nous allons dessiner.

Quand on travaille en trois dimensions (3D), en plus des deux axes de coordonnées, on a un troisième axe de coordonnées Z, exprimant la profondeur :
Dans ce cas précis, on utilise la commande size avec un troisième paramètre indiquant que l'on travaille dans un espace en 3D size(100, 100, P3D);
II-A-2. Connaître la taille de l'espace de dessin▲
Au sein d'un programme, on peut connaître à tout moment la taille de l'espace de dessin utilisé au moyen des mots-clés width et height. Ces instructions sont très utiles lorsque l'on souhaite notamment dessiner des formes qui puissent s'adapter ultérieurement aux éventuels changements de dimension de la fenêtre de visualisation.
II-B. Les formes▲
Beaucoup de formes prédéfinies sont fournies par Processing. En voici les principales :
II-B-1. Le point▲
Pour commencer à dessiner, nous allons partir d'un point. Sur l'écran, un point est l'équivalent d'un pixel localisé dans la fenêtre de visualisation par deux axes de coordonnées, x et y correspondant respectivement à la largeur (axe horizontal) et à la hauteur (axe vertical) de l'espace de dessin. En suivant ce principe, la création d'un point dans Processing s'effectue à l'aide de l'instruction point(x,y). Dans cet exemple, le point est très petit. Il est placé au centre de la fenêtre de visualisation.
point(50, 50);
Notez que le cadre de la fenêtre de visualisation (l'espace de dessin) a une dimension de 100 × 100, ce qui explique que le point soit situé en plein milieu. Si on le dessinait en dehors du cadre (hors champ), avec par exemple l'instruction size(150,150), on ne le verrait pas.
II-B-2. La ligne▲
Par définition, une ligne (AB) est constituée par une infinité de points entre un point de départ A et un point d'arrivée B. Pour la construire, nous allons nous intéresser uniquement aux coordonnées x et y de A et de B. Ainsi, si par exemple dans la fenêtre par défaut, le point A se situe dans la région en bas à gauche de votre fenêtre, et que le point B se situe en haut à droite, les instructions suivantes, peuvent dessiner cette ligne sous la forme line(xA,yA,xB,yB) :
line(15, 90, 95, 10);
II-B-3. Le rectangle▲
Un rectangle se dessine par quatre valeurs en faisant l'appel de rect(x,y,largeur,hauteur). La première paire de valeurs x et y, par défaut (mode CORNER) correspond au coin supérieur gauche du rectangle, à l'instar du point. En revanche la seconde paire de valeurs ne va pas se référer à la position du coin inférieur droit, mais à la largeur (sur l'axe des x, horizontal) et à la hauteur (sur l'axe des y, vertical) de ce rectangle.
Exemple :
rect(10, 10, 80, 80);
Comme les deux dernières valeurs (largeur et hauteur) sont identiques, on obtient un carré. Amusez-vous à changer les valeurs et observez-en les résultats.
Pour que la première paire de valeurs corresponde au centre (le croisement des deux diagonales aux coordonnées 50, 50) du rectangle, il faut utiliser le mode CENTER comme suit :
rectMode(CENTER);
rect(50, 50, 80, 40);Cela donne le résultat identique à l'exemple précédent.
II-B-4. L'ellipse▲
Comme pour le rectangle, l'ellipse se construit sous les modes CENTER (par défaut), et CORNER. Ainsi l'instruction suivante produit un cercle dont les coordonnées du centre sont les deux premières valeurs entre parenthèses. La troisième valeur correspond à la grandeur du diamètre sur l'axe horizontal (x) et la quatrième à la grandeur du diamètre sur l'axe vertical : notez que si les 3e et 4e valeurs sont identiques, on dessine un cercle et dans le cas contraire, une ellipse quelconque :
ellipse(50, 50, 80, 80);Amusez-vous à faire varier les 3e et 4e valeurs et observez-en les résultats.

II-B-5. Le triangle▲
Le triangle est un plan constitué de trois points. L'invocation de triangle(x1,y1,x2,y2,x3,y3) définit les trois points de ce triangle :
triangle(10, 90, 50, 10, 90, 90);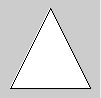
II-B-6. L'arc▲
Un arc ou section de cercle, peut se dessiner avec l'appel de arc(x, y, largeur, hauteur, début, fin), où la paire x, y définit le centre du cercle, la seconde paire ses dimensions et la troisième paire, le début et la fin de l'angle d'arc en radians :
arc(50, 50, 90, 90, 0, PI);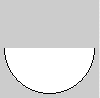
II-B-7. Le quadrilatère▲
Le quadrilatère se construit en spécifiant quatre paires de coordonnées x et y sous la forme quad(x1,y1,x2,y2,x3,y3,x4,y4) dans le sens horaire :
quad(10, 10, 30, 15, 90, 80, 20, 80);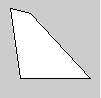
II-B-8. Courbe▲
Une courbe se dessine à l'aide de curve(x1, y1, x2, y2, x3, y3, x4, y4), où x1 et y1 définissent le premier point de contrôle, x4 et y4 le second point de contrôle , x2 et y2 le point de départ de la courbe et x3, y3 le point d'arrivée de la courbe :
curve(0, 300, 10, 60, 90, 60, 200, 100);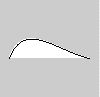
II-B-9. Courbe Bézier▲
La courbe de type Bézier se construit à l'aide de bezier(x1,y1,x2,y2,x3,y3,x4,y4)
bezier(10, 10, 70, 30, 30, 70, 90, 90);
II-B-10. Courbe lissée▲
L'appel de curveVertex() dessine plusieurs paires de coordonnées x et y, entre deux points de contrôle, sous la forme curveVertex(point de contrôle initial,xN,yN,xN,yN,xN,yN, point de contrôle final) ce qui permet de construire des courbes lissées :
beginShape();
curveVertex(0, 100);
curveVertex(10, 90);
curveVertex(25, 70);
curveVertex(50, 10);
curveVertex(75, 70);
curveVertex(90, 90);
curveVertex(100, 100);
endShape();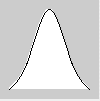
II-B-11. Formes libres▲
Plusieurs formes libres peuvent être dessinés par une succession de points en utilisant la suite d'instructions beginShape(),vertex(x,y),…,endShape(). Chaque point se construit par ses coordonnées x et y. La fonction CLOSE dans endShape(CLOSE) indique que la figure sera fermée, c'est-à-dire que le dernier point sera relié au premier, comme dans l'exemple ci-dessous de dessin d'un hexagone :
beginShape();
vertex(50, 10);
vertex(85, 30);
vertex(85, 70);
vertex(50, 90);
vertex(15, 70);
vertex(15, 30);
endShape(CLOSE);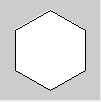
II-B-12. Contours▲
Vous avez remarqué que jusqu'à présent, toutes les figures données en exemple comportent un contour, ainsi qu'une surface de remplissage. Si vous voulez rendre invisible le contour, utilisez noStroke() en faisant bien attention de le placer avant la forme à dessiner :
noStroke();
quad(10, 10, 30, 15, 90, 80, 20, 80);
II-B-13. Remplissage▲
De la même manière, il est possible de dessiner des formes sans surface de remplissage avec l'instruction noFill() :
noFill();
quad(10, 10, 30, 15, 90, 80, 20, 80);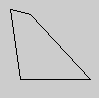
Par défaut, l'arrière-fond de la fenêtre de visualisation (l'espace de dessin) est gris neutre, les contours des figures sont noirs, et la surface de remplissage est blanche. Vous apprendrez au prochain chapitre comment modifier les couleurs à votre convenance.
II-B-14. Primitives 3D▲
Les formes prédéfinies disponibles en trois dimensions (primitives 3D) peuvent être réalisées de manière simple en appelant size(x, y, P3D) au début de notre sketch puis en employant en fonction de vos besoins les instructions sphere(taille) et box(longueur, largeur, profondeur). Il est également possible de produire des effets d'éclairage sur nos formes tridimensionnelles à l'aide de lights().
- La sphère
size(100, 100, P3D);
noStroke();
lights(); // éclairer l'objet 3D
translate(50, 50, 0); // voir Chapitre "Transformations"
sphere(28);
- La boîte
size(100, 100, P3D);
noStroke();
lights();
translate(50, 50, 0);
rotateY(0.5);
box(40);
II-C. Les couleurs▲
Dessiner une image à l'écran, c'est changer la couleur des pixels. Les pixels sont des petites zones, le plus souvent carrées, qui possèdent une couleur. Chaque couleur se définit par trois canaux qui sont le rouge, le vert et le bleu. Une valeur de 100 % de chacun de ces trois canaux donne du blanc. Une valeur de 0 % de chacun de ces trois canaux donne du noir. Il s'agit de lumière, et non de peinture. Ainsi, plus la valeur de chaque canal sera importante, plus la couleur sera lumineuse.
Par exemple, 100 % de rouge, 80 % de vert et 20 % de bleu vont donner ensemble la couleur orange. La méthode fill() nous permet de spécifier la couleur des prochaines formes à dessiner. Chaque canal d'une couleur peut être donné sur une échelle de 0 à 255. Ainsi, 80 % de 255 donne 204, et 20 % de 255 donne 51.
II-C-1. La couleur de fond▲
On peut changer la couleur de fond en appelant la méthode background(). Attention : rajouter background() à la suite d'une composition déjà existante, l'effacerait !
background(0, 0, 0);
II-C-2. La couleur de remplissage▲
À chaque fois que l'on dessine une forme, on le fait avec la couleur de remplissage qui est choisie à ce moment-là. On le fait en appelant la méthode fill().

noStroke();
fill(255, 204, 51);
rect(25, 25, 50, 50);Processing nous offre différents formats pour exprimer la couleur. Si vous faites de la programmation web, vous connaissez sans doute le format hexadécimal. Selon ce procédé, la même couleur orange peut être obtenue en écrivant :
fill(#ffcc33);
rect(25, 25, 50, 50);Par ailleurs, il est possible de spécifier la valeur du canal alpha de la couleur utilisée, c'est-à-dire son degré de transparence. Pour ce faire, on doit donc préciser quatre paramètres à la méthode fill(). Le quatrième argument est la valeur alpha.
noStroke();
fill(255, 204, 51); // orange
rect(25, 25, 50, 50);
fill(255, 255, 255, 127); // blanc semi-transparent
rect(35, 35, 50, 50);
Si l'on souhaite choisir une couleur qui correspond à un ton de gris, il suffit de donner un seul paramètre à la méthode fill(). C'est la valeur de gris, de 0 à 255.

fill(127);
rect(25, 25, 50, 50);On peut désactiver le remplissage des formes en appelant la méthode noFill().
II-C-3. La couleur du contour▲
Pour changer la couleur du contour des formes que l'on dessine, on doit appeler la méthode stroke() avec comme paramètres les canaux de la couleur désirée. Appeler noStroke() désactive la couleur de contour. À titre d'illustration, voici un dessin de masque africain utilisant ces deux instructions :
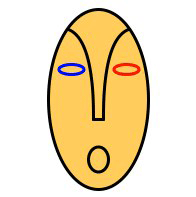
size(200, 200);
smooth();
background(255); // on dessine un fond blanc
stroke(#000000); // le contour sera noir
fill(#FFCC66); // le remplissage sera jaune
strokeWeight(3);
translate(width / 2, height / 2);
ellipse(0, 0, 100, 180); // forme elliptique du masque
ellipse(0, 60, 20, 25); // ellipse de la bouche
stroke(255, 0, 0); // le contour sera rouge
ellipse(28, -30, 25, 10); // ellipse de l'oeil droit
stroke(0, 0, 255); // le contour sera bleu
ellipse(-27, -30, 25, 10); // ellipse de l'oeil gauche
noFill(); // les prochaines formes n'auront pas de remplissage
stroke(#000000); // le contour des prochaines formes sera noir
bezier(-30, -70, -5, -60, -5, 0, -5, 20); // courbe du sourcil droit
bezier(30, -70, 5, -60, 5, 0, 5, 20); // courbe du sourcil gauche
line(-5, 20, 5, 20); // ligne du nez pour joindre l'extrémité des courbesII-C-4. La portée des modifications de couleur▲
Par défaut, toute modification de style (couleur de remplissage ou de contour, épaisseur ou forme de trait) s'appliquera à tout ce que vous dessinerez ensuite. Pour limiter la portée de ces modifications, vous pouvez les encadrer par les commandes pushStyle() et popStyle().
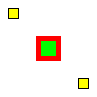
size(100, 100);
background(255);
stroke(#000000);
fill(#FFFF00);
strokeWeight(1);
rect(10, 10, 10, 10);
pushStyle(); // On ouvre « une parenthèse » de style
stroke(#FF0000);
fill(#00FF00);
strokeWeight(5);
rect(40, 40, 20, 20);
popStyle(); // On ferme notre parenthèse de style
rect(80, 80, 10, 10);Exercice :
Supprimez les commandes pushStyle() et popStyle() et observez la différence de comportement.
II-C-5. L'espace colorimétrique▲
Définir des couleurs à partir des canaux rouge, vert et bleu constitue un moyen parmi d'autres de décrire l'espace colorimétrique de votre dessin. Processing supporte également le mode TSV. TSV signifie « teinte, saturation, valeur ». En anglais, on appelle ce mode HSB, pour « hue, saturation, brightness ». On choisit une échelle de 0 à 100 pour chacun de ces trois canaux. La teinte correspond à un chiffre indiquant la position de la couleur sur l'échelle chromatique, soit un arc-en-ciel. Le rouge est à gauche, puis viens l'orange, le jaune, le vert, le bleu et le violet.
La méthode colorMode() est utile pour changer l'échelle numérique que l'on utilise pour spécifier les couleurs, et pour changer d'espace colorimétrique. Par exemple, appeler colorMode(RGB, 1.0), va changer l'échelle que l'on utilise pour spécifier chaque canal des couleurs afin qu'il aille de zéro à un.
Ici, on change le mode de couleur pour le TSV afin de créer un dégradé de teinte qui ressemble aux couleurs d'un arc-en-ciel.

noStroke();
size(400, 128);
// La teinte sera spécifiée avec un chiffre de 0 à 400
colorMode(HSB, 400, 100, 100);
// On fait quatre cents répétitions
for (int i = 0; i < 400; i++) {
fill(i, 128, 128);
rect(i, 0, 1, 128);
}II-D. Le texte▲
On va maintenant dessiner des caractères textuels qui s'afficheront dans la fenêtre de visualisation. Attention : écrire dans l'espace de dessin ne ressemble pas à l'écriture dans le sens classique du terme, notamment comme dans un traitement de texte. Le texte dans Processing ressemblerait plutôt à du « graffiti urbain », c'est-à-dire à une sorte de peinture de caractères alphanumériques qui finiront tous par s'empiler les uns sur les autres. C'est davantage un procédé « typographique » qu'un travail d'écriture, avec une insistance sur l'aspect graphique des mots ou des lettres que nous allons dessiner.
II-D-1. Bonjour Processing !▲
Tout comme les formes prédéfinies, telles les lignes ou les ellipses, il suffit d'une seule instruction dans notre sketch pour dessiner du texte. Ouvrez une nouvelle fenêtre d'édition, tapez la ligne suivante, et exécutez-la en cliquant sur le bouton run :
text("Salut!", 10, 20);Vous devriez voir s'afficher la petite fenêtre de visualisation par défaut de 100 × 100 pixels, avec le mot « »Salut ! » écrit en blanc :

Comme son nom l'indique, l'instruction text() dessine du texte dans la fenêtre de visualisation. Elle requiert trois paramètres : {le message que nous voulons écrire}, {sa coordonnée x}, {sa coordonnée y}.
Ce texte peut également être coloré, comme n'importe quelle forme géométrique, en changeant la couleur de remplissage :
fill(0);
text("Salut", 10, 20);
fill(255);
text("tout", 10, 40);
fill(255,0,0);
text("le", 10, 60);
fill(0,0,255);
text("monde", 10, 80);Ce programme devrait vous donner le résultat suivant, avec chacun des quatre mots écrits avec leur propre couleur :
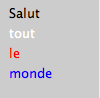
Il suffit d'indiquer une couleur, puis dessiner du texte avec cette couleur. Bien sûr vous pouvez ne choisir qu'une seule couleur et dessiner plusieurs messages avec cette couleur, ou dessiner avec une combinaison de couleurs comme dans cet exemple.
II-D-2. Empilement▲
Comme nous l'avons indiqué dans l'introduction de ce chapitre, les mots s'inscrivent à l'intérieur de la fenêtre de visualisation tel un dessin et non pas tel un système de traitement de texte. On ne peut ni sélectionner ni modifier directement ce texte à l'aide de la souris ou du clavier. La seule modification qui peut être appliquée s'effectue au niveau de votre programme en précisant à l'aide d'instructions appropriées que vous souhaitez par la suite effacer complètement le texte et d'écrire par-dessus.
Voici une illustration rapide de ce principe de superposition :
fill(0);
text("un mot peut", 10, 20);
text("en cacher", 10, 40);
fill(204);
rect(28,25,50,20);
fill(0);
text("un autre", 10, 60);
fill(255, 255, 255);
text("un autre", 11, 61);Nous avons écrit quatre messages, parfois avec la même couleur, parfois avec une autre. Notez que le mot « cacher » a été caché justement par la couleur de remplissage qui a été définie avec la même valeur que celle utilisée pour dessiner le fond.
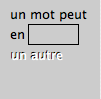
Comme dans n'importe quel dessin, l'ordre des opérations est important pour déterminer le rendu final. Ce principe s'applique même en dehors du logiciel Processing : « s'habiller, sortir, aller au travail » ne donnera pas le même résultat que « sortir, aller au travail, s'habiller ».